L'indice di Curtosi: Teoria e applicazioni pratiche
Articolo a cura di Corrado Fantini & Luca Pirazzoli
L'indice di Curtosi
L’indice di Curtosi è un indice che in statistica determina la forma di una distribuzione di frequenza e che misura lo "spessore" delle code di una funzione di densità, ovvero il grado di "appiattimento" di quest’ultima.
Il coefficiente di Curtosi è molto diffuso nei fondi d’investimento in quanto misura, attraverso dati superiori o inferiori a 0, in che modo si manifesta un fenomeno statistico.
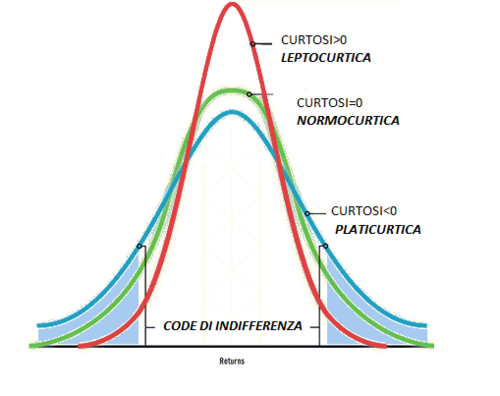
Dalla rappresentazione grafica della gaussiana è possibile percepire, anche visivamente, la positività o negatività di questo indice.
In questo senso la funzione di Gauss può assumere 3 formazioni: LEPTOCURTICA, NORMOCURTICA O PLATICURTICA.
Generalmente dall’analisi di un fenomeno statistico che può essere la temperatura atmosferica nell’arco di un mese o, come in questo caso, le performances di una strategia che vanno a formare una equity line, è possibile farsi una idea di come il suddetto fenomeno possa distribuirsi nel tempo.
Dal punto di vista grafico, come è possibile vedere dall’immagine a lato, si possono presentare tre tipi di scenari:
1- La curva LEPTOCURTICA (molto concentrata intorno alla sua media)
2- La curva NORMOCURTICA (normalmente concentrata intorno alla media)
3- La curva PLATICURTICA (poco concentrata intorno alla media)
Di conseguenza ad un valore dell'indice di Curtosi >0 corrisponde una gaussiana LEPTOCURTICA, se pari a 0 NORMOCURTICA e, contrariamente, ad valore <0 corrisponde per logica una gaussiana PLATICURTICA.
Un'applicazione pratica
Come di consueto proponiamo un’applicazione pratica di questo indice. Vediamo come creare valore aggiunto dall’analisi curtosica di una strategia operativa.
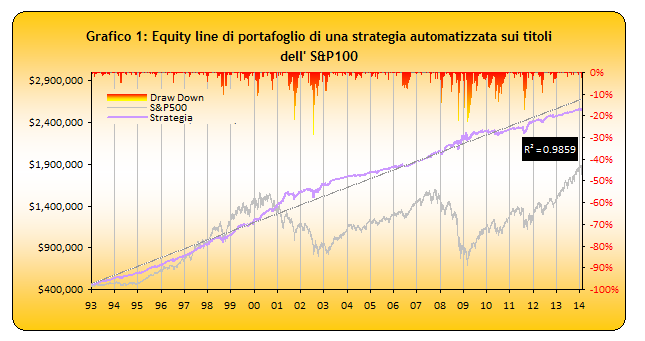
Prendendo come riferimento una delle nostre logiche di trading meccanizzato che lavora sulle azioni costituenti l'indice S&P100 (Grafico n. 1), abbiamo ricavato le performances mensili del portafoglio ottenuto dall'aggregazione delle singole equity lines out-of-sample componenti il paniere.
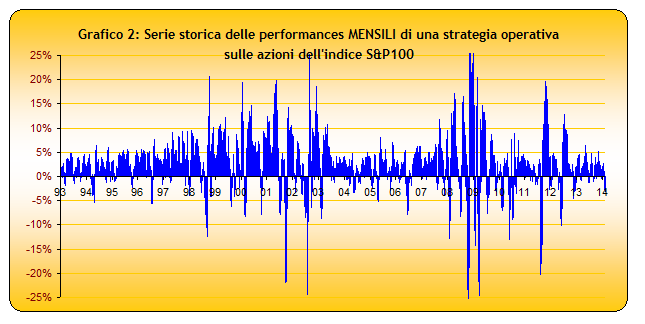
Partendo dallo storico di questa serie (si veda il Grafico n. 2) abbiamo ottenuto, per interpolazione, la distribuzione di frequenza delle varie classi.
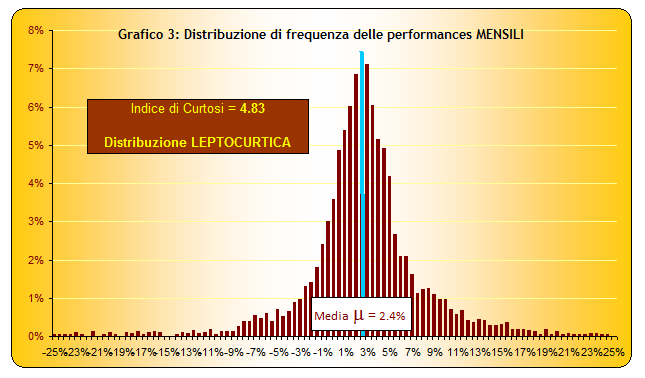
Nel Grafico n. 3, infatti, troviamo nell'asse delle ascisse le classi relative alle variazioni mensili osservate nel passato (contenute fra gli estremi -25% e +25%). Ad ogni classe corrisponde la rispettiva frequenza relativa che si può ricavare nell'asse delle ordinate.
La formula dell’indice di Curtosi
La formula per ricavare l’indice di Curtosi è la seguente:

Vedi anche:
Contributi in Traderpedia
- R-squared o coefficiente di determinazione
- Peak to peak (PTP) e Peak to valley (PTV)
- Over-fitting: che cosa significa?
- L'indice di Curtosi: Teoria e applicazioni pratiche