Regressione Lineare
La linea di regressione o regressione lineare, è l’unica linea che minimizza la media delle distanze fra la linea stessa e i punti di una curva.
Nel nostro caso la curva è quella dei prezzi ,mentre la linea di regressione è un segmento di regressione che comprende N barre-prezzo.
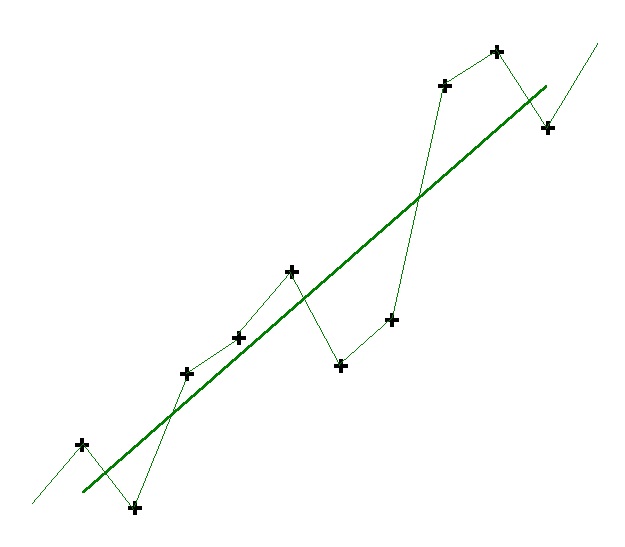
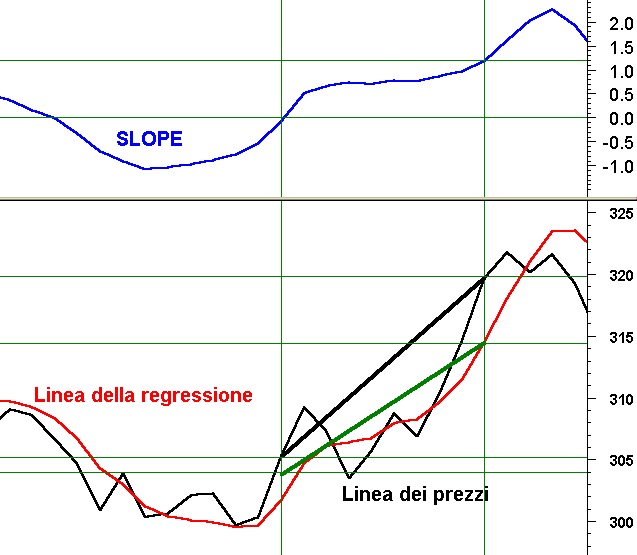
Possiamo avere un esempio in Fig. 1 in cui consideriamo una linea spezzata presa in un dato intervallo di tempo.
Dal punto di vista grafico si troverà un segmento le cui ordinate sono in media le più vicine alle ordinate degli N punti della spezzata ( regressione di Y su X ), con x che assume i valori dei periodi e con y che assume quelli dei valori di prezzo.
Quando la linea è in posizione , possiamo notare che, nell’intervallo considerato, la sua inclinazione è quella della tendenza della serie dei punti.
Se ci spostiamo nel tempo, l’inclinazione del segmento di regressione varierà conseguentemente alla posizione dei punti della curva alla quale deve adattarsi.
La funzione del MetaStock® che traccia la linea di regressione crea un segmento che comprende un numero N di barre-prezzo a piacere.
Opportunamente manovrato ,questo segue l’andamento dei prezzi e in pratica adatta un segmento ai punti dei dati.
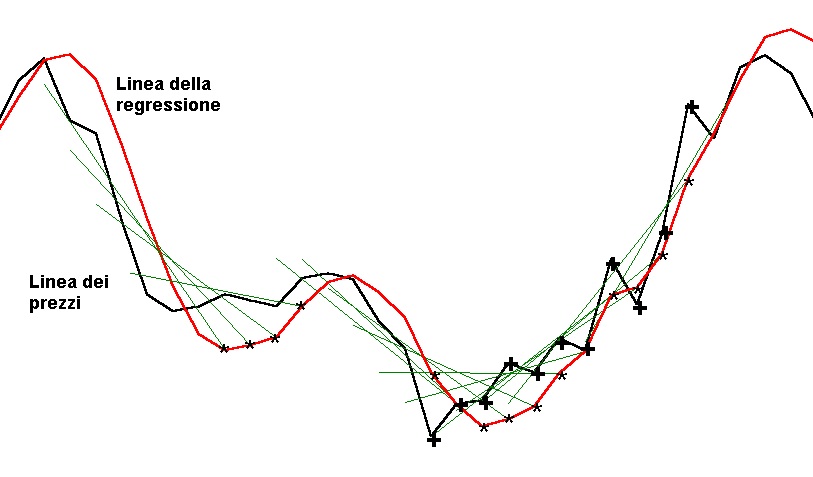
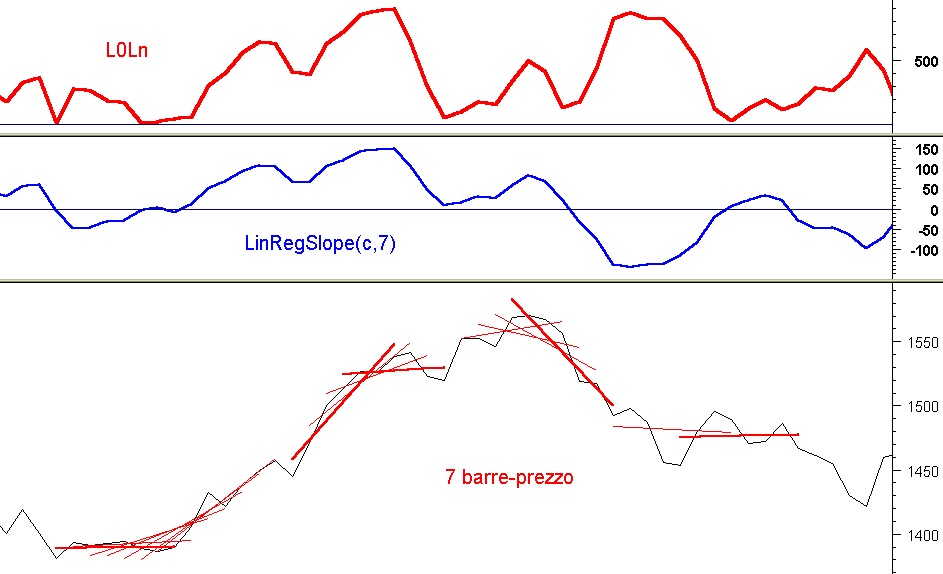
In Fig 2 possiamo notare che, mentre la serie dei prezzi forma una linea spezzata , chiamata linea dei prezzi , l’ultimo punto del segmento ne forma conseguentemente un’altra , chiamata linea della regressione lineare.
Ora introduciamo il concetto di incremento frazionato di regressione, che in inglese viene chiamato SLOPE (inclinazione, pendenza).
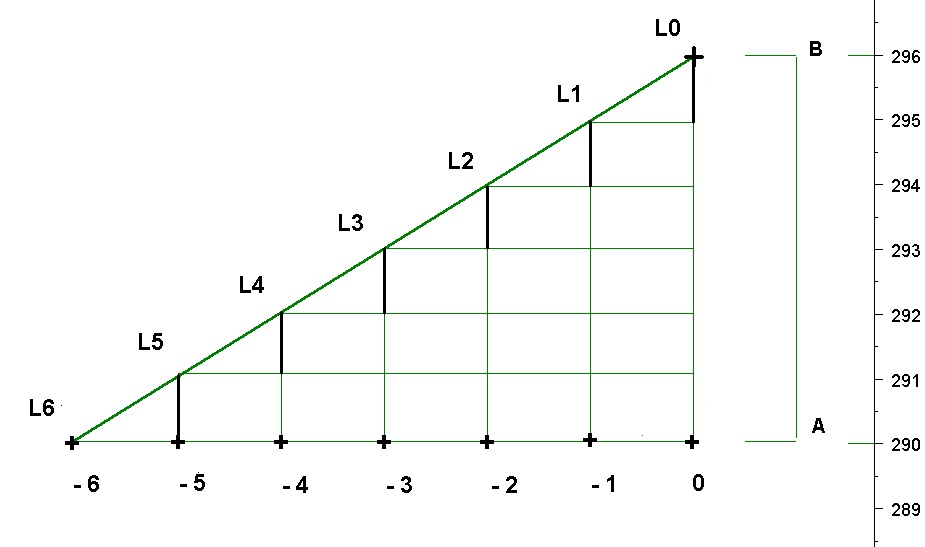
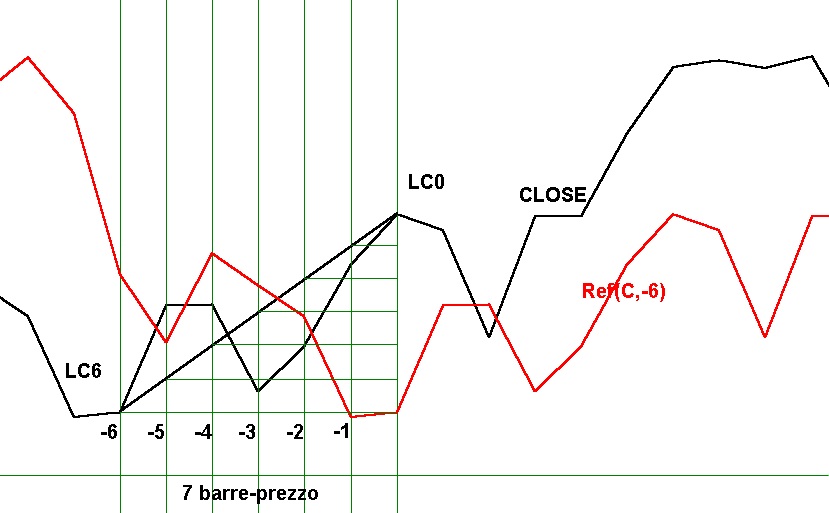
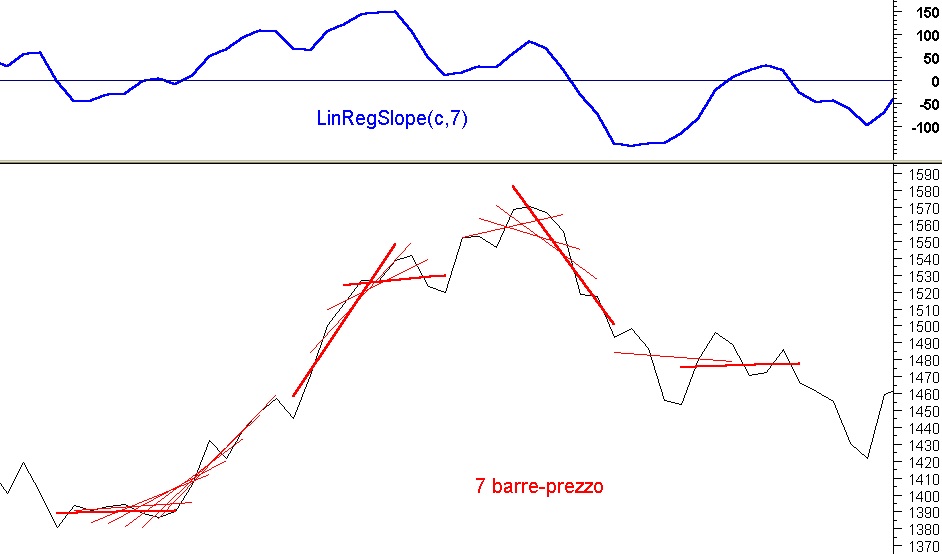
Per spiegarlo ci poniamo queste domande con riferimento alla Fig 3 che considera un segmento inclinato che va da L0 a L6 comprendendo 7 punti e immaginiamo il segmento fermo nella sua posizione ed un punto L che si muove di periodo in periodo lungo la sua lunghezza L0Ln:
1) di quanto è salito ( sceso ) il punto L dalla posizione L6 a quella di L0?
2) di quanto è salito ( sceso ) il punto L dalla posizione L6 a quella di L0, tenendo conto del numero 7 di punti in corrispondenza dei quali è stato tracciato il segmento?
Nel primo caso, avremo che il valore di L è variato di AB = 296-290 = 6 .
Nel secondo, il corrispondente valore dell’incremento frazionato = SLOPE è pari a AB / 6 = 6/6 = + 1.
Possiamo dire che L sale, in media , di 1 punto per ogni barra-prezzo nell’intervallo considerato.
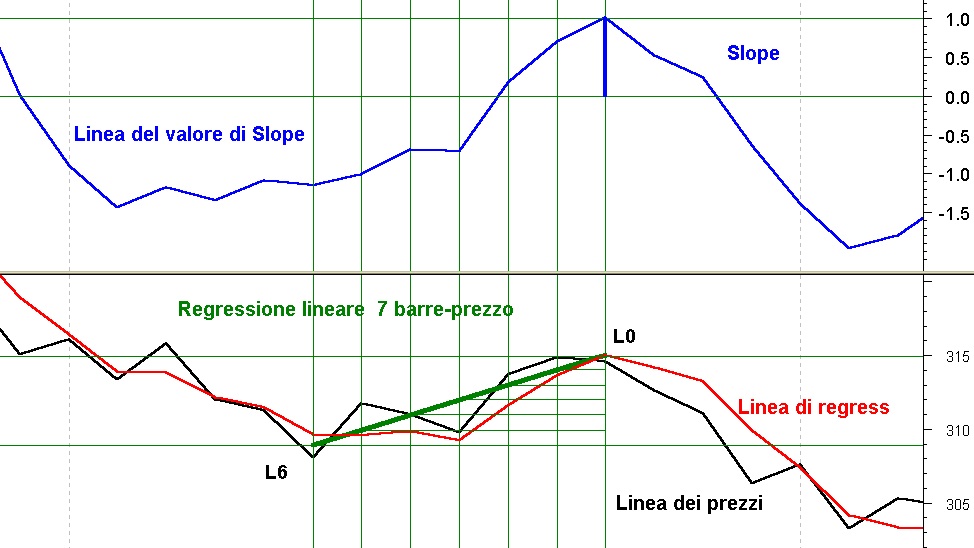
In Fig.4 possiamo notare che il valore di SLOPE in corrispondenza di L0 ha valore SLOPE = 1 dato dal rapporto della elevazione del segmento di regressione in corrispondenza di L0 diviso per il numero delle frazioni di elevazione ,in questo caso 6:
(315-309 ) / 6 = 6 / 6 = 1
Quando si calcola lo Slope, dobbiamo immaginare un segmento L0Ln fermo nell’istante 0 e quando si parla di L6 non si intende il valore che aveva L0 6 barre-prezzo prima, ma il valore effettivo di L in L6.
In altre parole, non dobbiamo confondere il valore di L6 con quello che aveva il valore del punto L0 del segmento di regressione 6 barre-prezzo prima, cioè in linea con L6.
Infatti, in Fig 4, seguendo a ritroso la linea della regressione fino al punto L6 possiamo notare che non vi è coincidenza di valori fra L6 del segmento e il suo corrispondente sulla linea di regressione tracciata dal movimento di L0 , 6 barre-prezzo prima.
In Fig 5 possiamo vedere la differenza esistente fra l’incremento di valore del prezzo e quello corrispondente del segmento di regressione nello stesso intervallo di tempo comprendente lo stesso numero di barre-prezzo.
Lo slope del prezzo è quindi diverso dallo slope del segmento di regressione.
Dato che il valore del prezzo in corrispondenza di L6 è quello della 6° barra-prezzo precedente, che si esprime con ref(c,-6), ed il valore del prezzo in corrispondenza di L0 è il prezzo corrente C (close), lo slope del prezzo sarà calcolato con:
(c-ref(c,-6)) / 6
(slope di C in corrispondenza della barra prezzo L0 ) Fig. 6
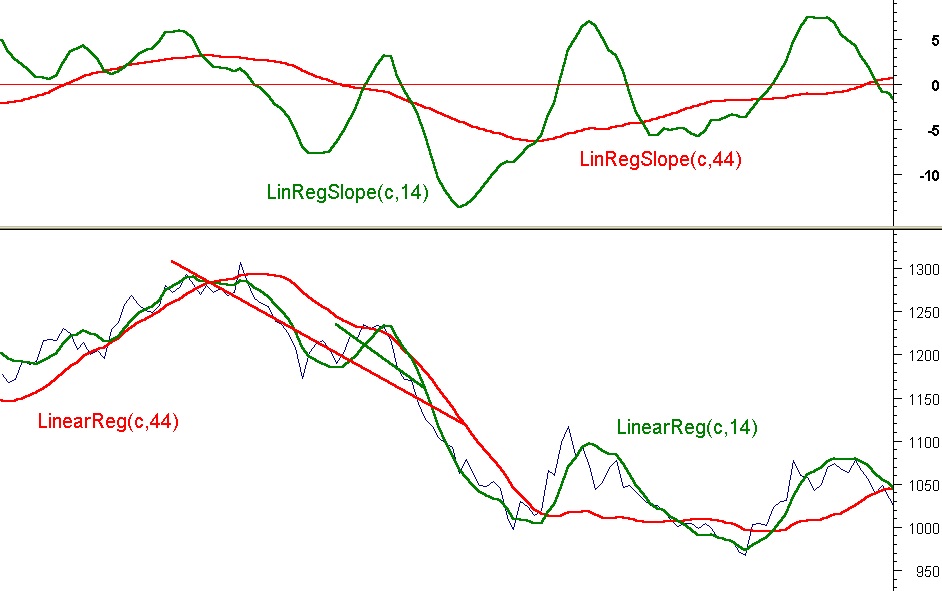
La linea della regressione generata dall’ultimo punto L0 del segmento di regressione può essere ottenuta mediante la funzione disponibile fra gli Indicatori:
LinearReg( C , 7 ) Figg. Precedenti
(valore del punto L0 del segmento di regressione lineare)
Lo slope del segmento di regressione può essere calcolato mediante la funzione, anch’essa disponibile fra gli Indicatori:
LinRegSlope( C ,7 ) Figg. 4,5
(slope della linea di regressione in corrispondenza della barra-prezzo L0)
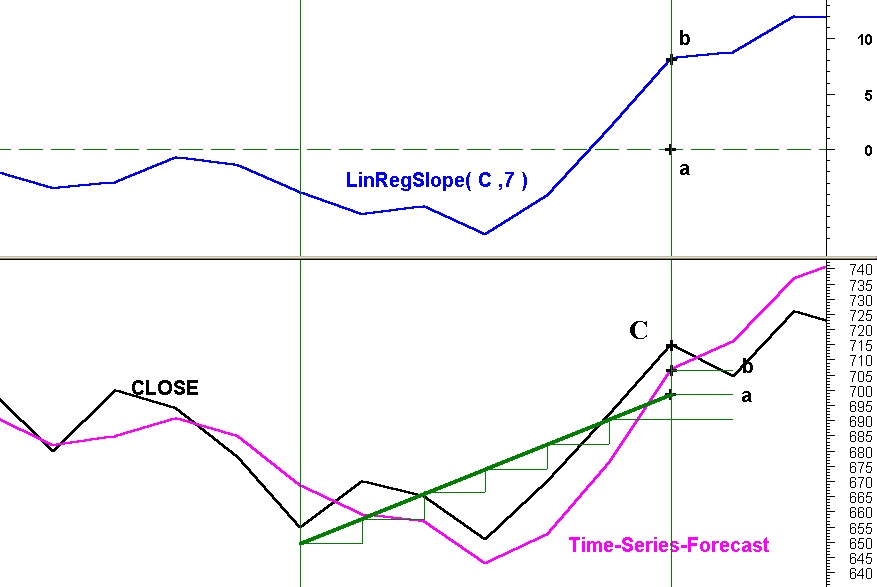
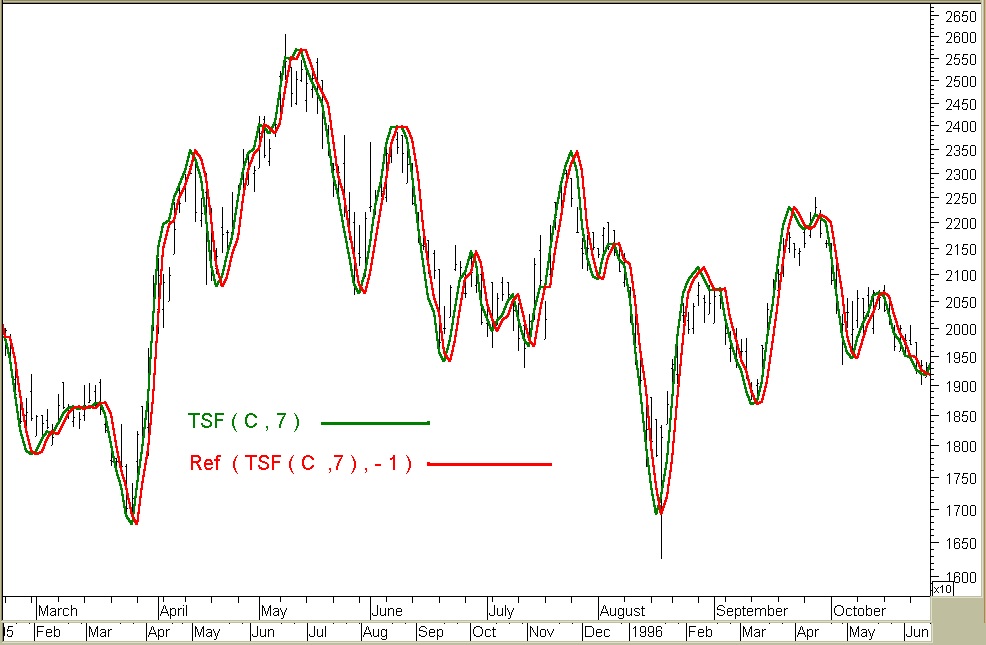
La funzione Time-Series-Forecast, in dotazione fra gli Indicatori , calcola il valore del punto L0 del segmento di regressione lineare e lo somma al valore del suo Slope.
In Fig. 7 viene evidenziato quanto ricavato con
TSF( C , 7 )
(time-series-forecast in corrispondenza del punto L0 del segmento di regressione)
equivalente alla somma
LinearReg( C , 7 ) + LinRegSlope( C ,7 )
oppure come Custom Formulas
MOV ( C , 7 , TIMESERIES )
o più semplicemente
MOV ( C , 7 , T )
Lo stesso risultato viene ottenuto mediante la funzione Moving Average, fra gli Indicatori, inserendo Time Series fra le opzioni Method e Close in Price Field.
Quest’ultima funzione permette, a differenza della precedente, la possibilità di inserire le opzioni Vertical o Horizontal Shift (spostamento verticale di un certo valore percentuale od orizzontale, in avanti o indietro nel tempo, di un numero intero di periodi rispetto a quello di riferimento)
Come abbiamo visto nelle formule precedenti, dobbiamo fare attenzione al giusto valore da inserire come parametro.
Nel caso del segmento di regressione, della linea del segmento di regressione,
dello slope del segmento di regressione, del timeseries forecast e nel Moving Average TimeSeries, trattandosi di funzioni relative ad un segmento di estremi L0 Ln, il valore di parametro da inserire sarà quello del numero di periodi o barre-prezzo compresi gli estremi, cioè N = n+1 .
Le Figg. 4,5,6,7 mostrano casi differenti ma significativi per evidenziare gli argomenti proposti.
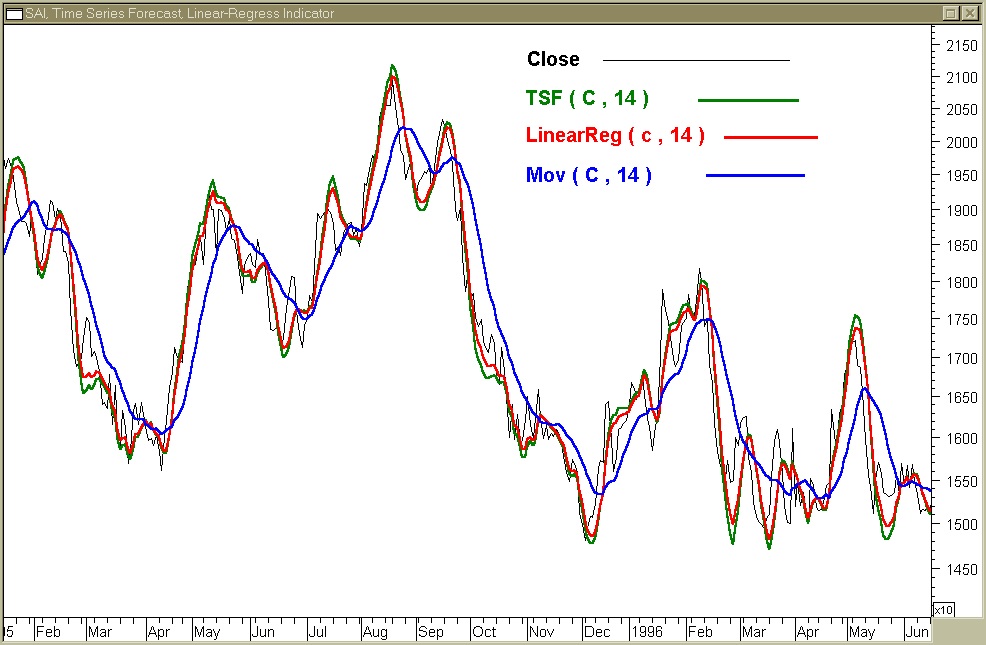
In Fig.8 possiamo vedere come non vi sia molta differenza fra la LinearReg. ed il TSF per lo stesso periodo tranne che il TSF è più sensibile alle variazioni dei prezzi.
Il vantaggio rispetto ad una media mobile di uguale periodo è evidente in Fig.8: i due metodi che usano il segmento di regressione lineare hanno poco ritardo sul today price, inoltre possiamo vedere che, nei tratti “tormentati“ del grafico del Close, seguono con decisione il trend principale, invertendo drasticamente direzione al momento opportuno con grande tempestività.
Il punto L0 del segmento di regressione segue il prezzo mentre la sua lunghezza, in termini di numero di barre-prezzo, fa da volano d’inerzia smorzando il suo andamento.
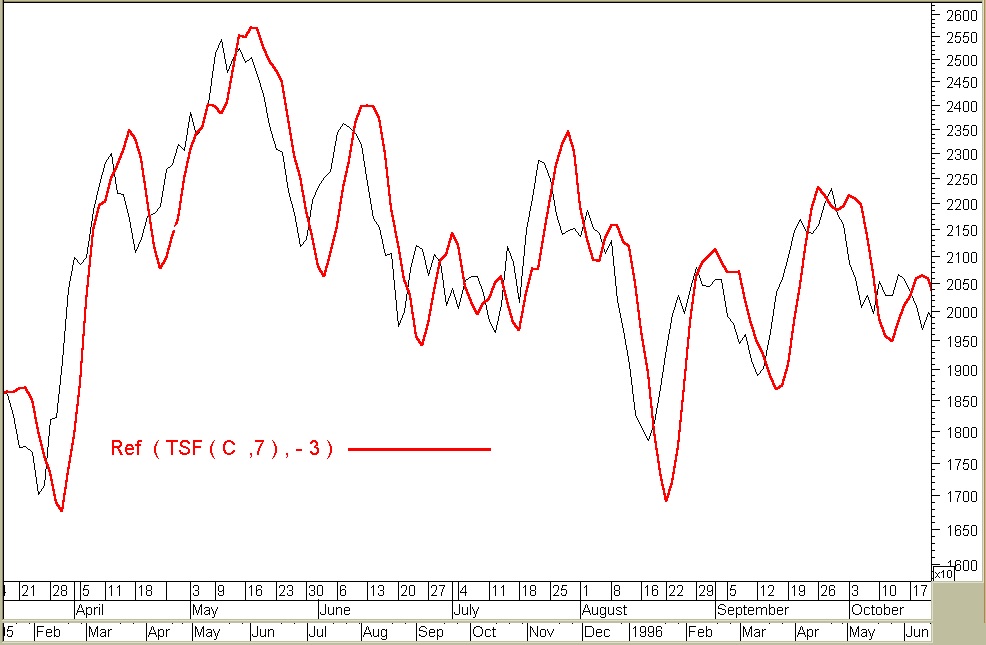
Il TSF, avendo in più lo SLOPE, è come se fosse avanti rispetto al today price dato che quest’ultimo rileva immediatamente ogni minima variazione .
Possiamo averne un esempio in Fig. 9 dove il TSF, anticipato di un periodo, fa da rilevatore di variazione rispetto al TSF che si trova sempre il sintonia con il trend.
Il vantaggio rispetto alle medie mobili risulta oltremodo evidente in Fig. 10, dove il TSF è stato anticipato di 3 periodi.
Ora mostreremo in che modo le funzioni che abbiamo visto precedentemente ci possono aiutare ad interpretare i movimenti dei prezzi .
Per fare questo prendiamo in considerazione le seguenti osservazioni:
1) Abbiamo visto che lo Slope del segmento di regressione lineare, in un dato istante, è il rapporto fra la variazione di L0 in termini di prezzo in un dato intervallo di tempo e la variazione del tempo, in termini di barre-prezzo, nell’intervallo considerato.
In altre parole lo Slope ci rappresenta la Velocità e la Direzione di L0.
Dato che L0 si muove in funzione del prezzo corrente C0, possiamo dire che lo Slope ci indica la velocità e la direzione del movimento in atto.
Dalla lunghezza N = numero di barre-prezzo che comprendono LoLn , dipende la tempestività del segnale, pur tenendo presente che valori di N troppo alti la diminuiscono e valori troppo bassi aumentano la variabilità dei segnali, Fig. 11.
Il valore di default per il MetaStock® è N = 14.
2) Facendo riferimento alla Fig. 12 , possiamo notare che, pur mantenendo costante la lunghezza del segmento di regressione lineare, in termini di barre-prezzo, la sua lunghezza reale, L0Ln, aumenta o diminuisce lungo il percorso della linea del prezzo.
Quando avviene un’inversione, L0Ln è minima, quando il movimento è definito in una direzione ed è ben impostato, la lunghezza L0Ln diventa massima.
In altre parole, la lunghezza reale L0Ln , in un dato istante in linea con L0, ci da un’indicazione della Forza del movimento in atto.
Unendo le due osservazioni possiamo dire che :
a) uno Slope positivo con lunghezza L0Ln crescente è indice di un movimento dei prezzi forte e ben impostato al rialzo;
b) uno Slope negativo con lunghezza L0Ln crescente è indice di un movimento dei prezzi forte e ben impostato al ribasso;
c) uno Slope positivo con lunghezza L0Ln in diminuzione ci indica che il movimento, anche se al rialzo, sta per esaurire la sua Forza;
d) uno Slope negativo con lunghezza L0Ln in diminuzione ci indica che il movimento, anche se al ribasso, sta per esaurirsi;
e) il raggiungimento di un valore massimo o minimo di L0Ln ci segnala un cambiamento di direzione del movimento per esaurimento;
f) la Velocità del movimento la possiamo quantificare dal valore dello Slope;
g) la Direzione del movimento la possiamo valutare dal valore algebrico dello Slope;
h) la Forza del movimento la possiamo desumere dal valore di L0Ln.
Vista l’utilità di queste ultime considerazioni, vediamo di costruire un indicatore che ci calcoli la lunghezza reale del segmento di regressione lineare in corrispondenza di un valore C0 del prezzo per poter valutare la forza del movimento in atto.
Facendo riferimento alle Figg. 3,4, consideriamo il segmento di regressione lineare come l’ipotenusa di un triangolo rettangolo, i cui cateti sono rappresentati rispettivamente da
AB = LinRegSlope( c , N ) * ( N - 1 ) e da n = ( N - 1 )
Per il teorema di Pitagora possiamo scrivere
L0Ln = radice quadrata di ( quadrato di ( AB ) + quadrato di ( N - 1 ) )
Da cui, in linguaggio MetaStock® avremo:
L0Ln = sqr( pwr( LinRegSlope( c , N ) * ( N - 1 ) , 2 ) + pwr( N - 1 , 2 ) )
Per un segmento di regressione lineare L0Ln comprendente N = 7 barre-
prezzo, in un intervallo di tempo n = 6 avremo che la sua lunghezza reale può essere calcolata mediante:
sqr( pwr( LinRegSlope( c , 7 ) * 6 , 2 ) + 36 ) Fig. 13
Come si può vedere dalla Fig.13, l’andamento dell’indicatore ottenuto come custom formulas mostra in modo chiaro la Forza del movimento in atto, mentre lo Slope ci mostra la Direzione e la Velocità.
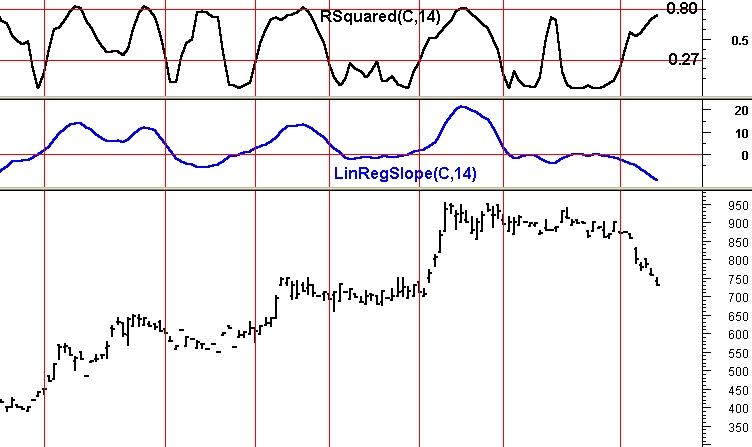
Il programma MetaStock® 6.0 offre un indicatore chiamato r-squared che ci calcola la Forza del movimento in percentuale da 0 a 1 per un segmento di regressione lineare di N barre-prezzo.
Rsquared( C , N )
Come il precedente, questo indicatore deve essere usato in abbinamento con il LinearRegSlope.
Il vantaggio rispetto alla misura della lunghezza del segmento di regressione è che l’ r-squared ci permette di valutare se il trend è statisticamente significativo.
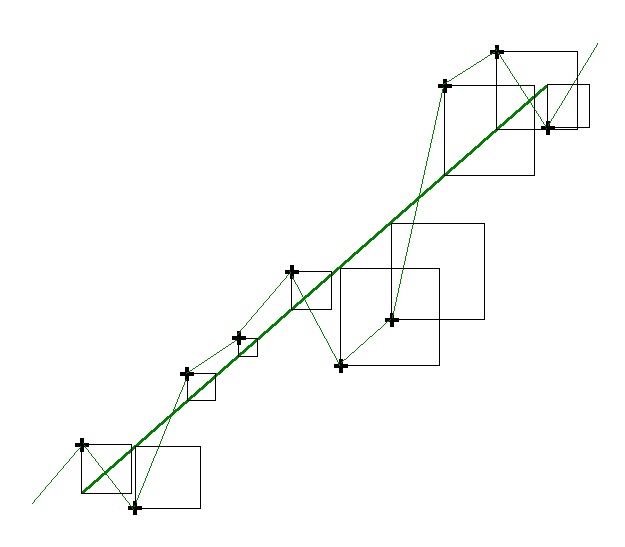
Senza entrare nei particolari di tipo analitico-matematico, possiamo semplicemente mostrare in Fig.14 il metodo di costruzione di un segmento di regressione di tipo lineare, chiamato metodo dei minimi quadrati.
Questo metodo trova la linea che minimizza la somma dei quadrati delle distanze dei suoi punti da quelli della curva a cui deve adattarsi.
In parole povere, trova le condizioni in cui vengono minimizzati gli errori di adattamento alla curva.
Questi errori, essendo in termini di differenza di prezzo , possono essere negativi o positivi.
Elevandoli alla seconda potenza (squaring) otterremo valori positivi.
Chiamando sqe la somma dei quadrati di tutti gli errori fra gli N dati e i suoi corrispondenti punti sul segmento ,se per ipotesi il segmento di regressione si sovrappone perfettamente alla curva dei prezzi , avremo
sqe = 0
cioè nessun errore.
In poche parole avremo il 100 % di linearità con il movimento in atto ed r-squared = 1.
Quindi, più il segmento di regressione risulta aderente al movimento in atto maggiore è il valore percentuale, da 0 a 1, di r-squared.
Diversamente, se il segmento di regressione lineare è poco aderente al movimento in atto, la somma dei quadrati degli errori fra la curva dei prezzi ed il segmento stesso è molto elevata, quindi avremo un valore di r-squared molto vicino a 0, Fig.14.
L’ r-squared viene chiamato coefficiente di determinazione della regressione lineare ed è in pratica una misura del grado di accostamento del segmento di regressione lineare alla curva dei prezzi.
Come abbiamo fatto notare nelle pagine precedenti, dal valore N delle barre prezzo che comprendono il segmento di regressione dipende la sua cosiddetta “inerzia”, però aumentando N aumenta la variabilità ed il numero dei dati su cui poter effettuare il calcolo degli scostamenti.
Statisticamente, più ampio è il numero degli elementi a disposizione, più affidabile diventa la valutazione.
Mediante una procedura di calcolo statistico, in funzione di N, si può individuare un valore critico al di sotto del quale avremo una vera e propria dispersione e l’accostamento sarà molto basso.
Per un dato valore di N , superando il valore critico, l’accostamento risulta via via più marcato fino a raggiungere un valore massimo, dopo di che avviene un’inversione. Maggiore è il numero N di barre-prezzo del segmento di regressione e più basso sarà questo valore critico.
Qui, riportata dal MetaStock® 6.0, mostriamo la tabella dei valori critici di r-squared in corrispondenza dei rispettivi valori di N :
N 5 10 14 20 25 30 50 60 120
r-squared 0.77 0.40 0.27 0.20 0.16 0.13 0.08 0.06 0.03
critical value
95% di attendibilità
In Fig.15 mostriamo un abbinamento dello Slope con r-squared, analogo a quello mostrato in Fig.13, con in più la possibilità di stabilire l'affidabilità
delle indicazioni di forza del trend quando r-squared supera il valore critico.
Possiamo notare che, quando lo Slope è positivo e l’r-Squared si trova sopra 0.8 ed ha invertito la rotta verso il basso, anche il movimento in atto sta per concludere il suo movimento al rialzo. Una conferma ulteriore verrà dallo Slope se invertirà la sua direzione e volgerà verso il basso
APPENDICE
Le formule mostrate fino ad ora sono asportabili ed utilizzabili con il programma di Analisi Tecnica “MetaStock® 6.0” e successivi.
Le seguenti Formule, altrettanto asportabili, sono per tutti coloro che possiedono le versioni precedenti.
Per ovvie ragioni di spazio e per essere in linea con le premesse, non mostreremo come sono state ottenute .
Anche se per molti risulteranno superate da quelle più sintetiche in uso alla versione 6.0 e successive, vi invitiamo ugualmente a provarle.
1) Lo Slope del segmento di regressione comprendente N barre-prezzo può
essere ricavato mediante:
(( N * (Sum(Cum(1) * C , N ))) - (Sum(Cum(1), N )*(Sum(C, N )))) /
(( N * Sum(Pwr(Cum(1),2), N ))-Pwr(Sum(Cum(1), N ),2))
2) La Linea della Regressione Lineare e cioè la “traccia” del punto L0, del
segmento di regressione L0Ln, che si muove in sintonia con il prezzo,
può essere ricavata mediante:
TSF(C,N)-(((N*(Sum(Cum(1)*C,N))) -(Sum(Cum(1),N) *(Sum(C,N)))) /
((N*Sum(Pwr(Cum(1),2),N))-Pwr(Sum(Cum(1),N),2)))
3) Il valore di r-squared, da utilizzare in abbinamento allo slope come
mostrato nelle pagine precedenti, può essere ottenuto mediante :
Pwr( Corr( Cum(1) , C , N , 0 ) , 2 ) .