Fibonacci
Leonardo di Pisa detto il Fibonacci, nato a Pisa intorno al 1170, è considerato il più grande matematico del Medioevo. Nella sua lunga permanenza presso Algeri, dove il padre era impiegato di dogana, ebbe modo di apprendere la numerazione araba e in seguito, viaggiando per il Mediterraneo, di conoscere le opere di Euclide e dei matematici arabi.
Le sue opere più importanti sono la Practica Geometrica e il Liber Abbaci, dove si introducono le proprietà della successione di numeri che prende il nome di Fibonacci; le cronache sottolineano che egli fece ritorno da un viaggio in Egitto con una misteriosa serie di numeri sviluppata partendo da ricerche sul tasso di riproduzione dei conigli.
La progressione è descritta nel capitolo XII del libro Liber Abbaci, in altre parole il libro è un abaco, ossia un "manuale per far di conto” scritto da Fibonacci nel 1228, in questo libro si pone un problema sul tasso di riproduzione dei conigli dalla cui soluzione deriva la famosa serie.
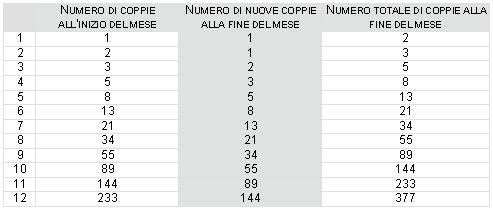
Il problema viene così impostato: "quante coppie di conigli si troveranno in un recinto dopo un periodo di 1 anno se nel primo mese si pone nel recinto una coppia e se si ipotizza che la coppia generi una nuova coppia di conigli ogni fine mese e che ogni nuova coppia generi un'altra coppia con lo stesso ritmo”?
Costruiamo una tabella per monitorare l'evoluzione del numero delle coppie.
La risposta al problema è 377, tuttavia non è questo il dato che interessa, ma la famosa progressione di Fibonacci che sta nella colonna di mezzo.
In Egitto, Fibonacci studiò a lungo la Grande Piramide di Giza e notò che gli antichi egizi avevano, forse consapevolmente, integrato la Golden Ratio, nella proporzione geometrica della piramide. Molti da allora hanno tentato di penetrare i segreti della Piramide di Giza, che differisce dalle altre piramidi per essere, più che una tomba, un irrisolvibile mosaico. In realtà, la piramide era stata disegnata in maniera tale che larea di ogni facciata fosse stato uguale al quadrato costruito sulla sua altezza.
La base della Piramide di Giza è pari a 783,3 piedi, mentre l'altezza è pari a 484,4 piedi: il rapporto fra le due misure è pari a 1,618, la Golden Ratio, appunto. E ancora, laltezza della piramide, in pollici, è pari a 5813 (5, 8, 13 sono numeri di Fibonacci). In sostanza, queste osservazioni hanno fatto limpressione della volontà, da parte degli antichi Egizi, di trasferire a noi i frutti della loro conoscenze avanzate in campo matematico.
Ma il discorso è più ampio, evidenze della serie di Fibonacci sono presenti in molti fenomeni naturali: i semi del girasole sono disposti su 89 curve, secondo il modello della spirale logaritmica, 55 in una direzione e 34 nell'altra; la struttura della spirale logaritmica (la più bella delle curve matematiche) è inoltre presente nel guscio della lumaca, nella ragnatela costruita da alcune specie di ragno, nella conformazione di alcune galassie, nell'orecchio umano e in tante altre meraviglie della natura. In anatomia, come si vede dall'esempio, l'ombelico è posizionato in corrispondenza del 61,8% dell'altezza totale dell'uomo.
Molti analisti hanno messo in relazione la misura e la durata dei movimenti dei prezzi delle azioni con i numeri di Fibonacci sviluppando dei tools grafici che considerano sia il prezzo che il tempo.