I quadrati. Il centro di gravità
«Ogni movimento nel mercato è il risultato di una legge naturale e di una Causa che esiste molto tempo prima che l’Effetto accada e può essere determinata con anni d’anticipo [...]. Ogni massimo o minimo importante più tardi diventa un importante centro di gravità nel successivo movimento [...]. Ogni cosa cerca il centro di gravità e si formano importanti massimi e minimi in base ai centri e alle misure del tempo da un centro, massimo o minimo [...]. Ogni cosa si muove in cicli come risultato della legge naturale di azione e reazione [...]. Non c’è nessun prezzo minimo o massimo che non possa essere determinato dalla matematica. Ogni movimento di mercato è il risultato di una Causa e una volta che determini la Causa è abbastanza facile sapere perché l’effetto è così». William D. Gann
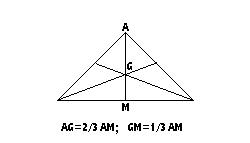
In geometria, il centro di gravità è rappresentato dal punto medio se si tratta di un segmento, dal baricentro se si tratta di una figura piana.
Così, il centro di gravità di un triangolo è il punto di intersezione delle mediane, il centro di gravità di un quadrato è il punto di intersezione degli assi e il centro di gravità del cerchio è il centro del cerchio. Il centro di gravità del triangolo ha la proprietà di dividere le mediane in due parti di cui l’una è il doppio dell’altra, cioè una parte vale 1/3 della mediana e l’altra parte vale 2/3 di tutta la mediana.
In fisica il centro gravità di un corpo è il punto in cui agisce la forza peso complessiva del corpo. Un corpo si trova in equilibrio stabile quando allontanando il corpo dalla posizione in cui esso vi ritorna. L’equilibrio è instabile quando anche per un piccolo spostamento il corpo si allontana definitivamente dalla posizione di equilibrio.
L’equilibrio è indifferente quando anche le posizioni vicine sono posizioni di equilibrio, cioè, comunque si sposti il corpo esso rimane in condizioni di stabilità.
Il tipo di equilibrio è legato alla posizione del corpo rispetto al suo centro di gravità.
Ad esempio, se un quadro è appeso con un chiodo sopra il suo centro di gravità allora l’equilibrio è stabile, infatti, se si sposta il quadro dalla verticale esso tende a recuperare la posizione oscillando attorno alla verticale. Se il quadro è appeso sotto il baricentro quando si sposta un po’ tende ad allontanarsi (si “capovolge”), l’equilibrio è instabile. Se il quadro è appeso piantando il chiodo sul baricentro, comunque si giri il quadro sul muro, il quadro rimane fermo, cioè l’equilibrio è indifferente.
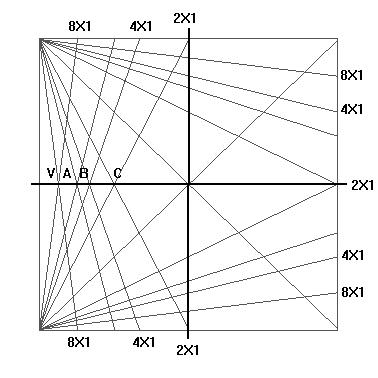
Le figure sono stati costruite con quadrati di 90x90, valori che per Gann costituiscono il “quadrato campione”. Sono stati tracciati poi i 4 assi del quadrato determinando il centro di gravità del quadrato, ossia il baricentro del quadrato. Prendendo il punto medio C tra il centro del quadrato e il punto V, sulla verticale e congiungendolo con il vertice sinistro del quadrato si forma il noto angolo 2x1.
Poi prendendo il punto medio B del segmento VC e congiungendolo con il vertice in basso a sinistra del quadrato otteniamo l’angolo 4x1, infine prendendo il punto medio A del segmento VB e congiungendolo con il vertice in basso a sinistra del quadrato si ottiene l’angolo 8x1. (Punto medio = centro di gravità).
Osservando attentamente la figura si può osservare che ripetendo la costruzione dei punti medi e congiungendo con il vertice in alto a sinistra del quadrato si ottengono tutti gli angoli. Tutte queste linee individuate, comprese le linee verticali e orizzontali, per Gann sono centri di gravità. L’angolo principale è quello di 45° che deve essere sempre tracciato per primo.
Il centro di gravità più importante e più forte, quindi, è il centro del quadrato perché è l’unico punto in cui convergono 4 angoli da 45°, due obliqui, uno orizzontale e uno verticale e, com’è noto, l’unione fa la forza.
Un’azione quando abbandona verso l’alto o verso il basso un angolo o centro di gravità tende ad allontanarsi da questo e stabilizzarsi, cioè tende a “cadere” verso il suo centro di gravità successivo. In fisica questa condizione è considerata di equilibrio instabile.
Un’azione che sosta su un angolo oscilla sempre vicino a quest’angolo, cioè fa quello che in fisica è definito equilibrio stabile. Chiaramente trattandosi di azioni e non di quadri appesi ad un muro, prima o poi lascerà questo centro di gravità. (Questo è causato dal fatto che anche per il Tempo esistono propri centri di gravità).
Un’azione che si trova su un centro di gravità lì si è stabilizzata, cioè fa un massimo o un minimo principale o secondario. Va ricordato che in analisi matematica i punti di massimo o di minimo relativi o assoluti sono anche detti punti stazionari. Quindi sugli angoli o centri di gravità ci si deve attendere un cambiamento del trend principale o del trend minore.
Infine, va tenuto presente che per centro di gravità non si deve pensare solo a particolari valori di prezzo, ma si devono considerare anche i valori di tempo, questi ultimi, per Gann, sono i più importanti, così egli ha scritto nel suo Stock Market Course: «Ho scoperto, dopo anni di esperienza, che in un lungo periodo di anni un’azione non può mantenere un guadagno di più di un punto al mese, o che non può fare di meglio che tenere l’angolo di 45°. Quando un’azione nei suoi primi anni sale troppo rapidamente e supera il tempo, devono accadere ripide reazioni mentre l’azione sta facendo quadrato o si sta aggiustando con il periodo di tempo. Una delle mie regole è, quando il Tempo e lo Spazio si bilanciano, l’azione fa un massimo o un minimo.
Abbiamo più volte ribadito che l’angolo più importante è l’angolo di 45°, perché in quest’angolo il Tempo e lo Spazio sono uguali, cioè fanno il quadrato. Se è vero che un’azione tende a stabilizzarsi sull’angolo di 45° adesso ci concentriamo sui tipi di grafico giornaliero, settimanale e mensile che tendono a stabilirsi su quest’angolo..
Supponiamo in via del tutto teorica che un’azione rimanga per un lungo periodo sull’angolo di 45° o 1x1 del grafico giornaliero, ciò significa affermare che essa cresce di 1 punto al giorno per un lungo periodo, cioè di 5 punti alla settimana e di 21-22 punti al mese, cioè che non si trova sull’angolo di 45° né sul grafico settimanale né tanto meno su quello mensile.
Allora se è vero che dopo un lungo periodo di anni l’azione tende a stabilizzarsi sull’angolo di 45° del grafico mensile vuol dire che non si trova sull’angolo di 45° né sul grafico settimanale né su quello giornaliero, perciò su questi grafici sta oscillando da un centro di gravità ad un altro. Questo spiega che le correzioni o le reazioni del mercato non sono altro che la quadratura dei periodi di tempo minori, cioè la tendenza a stabilizzarsi sull’angolo di 45°, e i grandi ribassi o le grandi salite non sono altro che la quadratura dei periodi di tempo maggiori. Questo spiega essenzialmente la causa dei movimenti azionari.