La matematica nelle perdite di borsa
anche se esso contrasta con la tua opinione del mercato e con la tua valutazione della domanda e dell'offerta.
(Jesse Livermore)
La matematica non è un'opinione, fino a qui siamo tutti d’accordo, ma è proprio quest’affermazione che in qualche modo ci espone al rischio, in particolare sulla gestione delle perdite di un trading system.
Se pensiamo alla matematica come scienza delle quantità, infatti, due più due fa universalmente quattro, ma questa non è l'unica funzione della matematica, essa è anche una scienza della relazione, ossia può determinare i rapporti che intercorrono tra diverse entità numeriche. Poiché le considerazioni sulle quantità sono più frequenti e pratiche di quelle sulla relazione noi abbiamo fissato nella memoria le prime e scordato, o quasi, le seconde.
Applicando successivamente le due diverse funzioni della matematica nelle quotazioni di borsa vediamo quanto diversi siano gli esiti. Se la borsa sale del 10% ed in seguito scende della stessa percentuale in termini di quantità la differenza è zero, naturalmente il risultato è valido anche nel caso contrario.
Ben diverso è invece il risultato se le variazioni percentuali le applichiamo in funzione della relazione, quindi in riferimento a qualche entità, ad esempio se investiamo 1.000€ e otteniamo un aumento del 10%, si raggiunge il nuovo importo di 1.100€, se poi questo capitale è interessato da un ribasso del 10% ci troviamo con un capitale di 990€.
La regola, ovviamente, è rispettata anche nel caso contrario, se oggi investo 1.000€ su un titolo che perde subito un 10% mi trovo con 900€. Il giorno successivo il titolo sale del 10% e arrivo a 990€, ossia con una perdita dell’1%.
Da ciò si può dedurre che in borsa se accade un rialzo a cui segue un ribasso della stessa percentuale, o viceversa, il risultato non sarà mai zero, ma sempre diverso da zero.
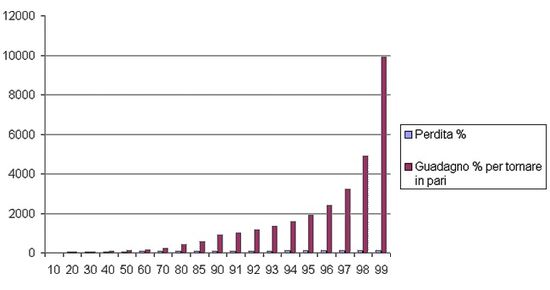
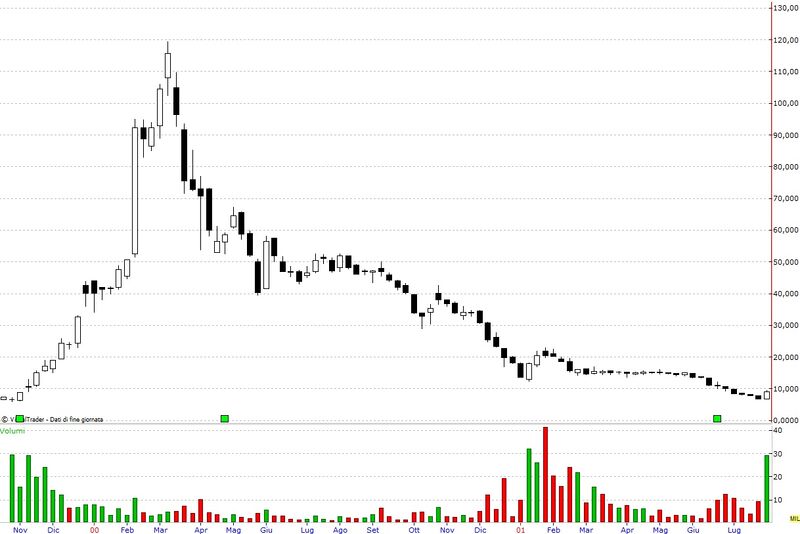
Purtroppo questo non è tutto. Se aumentiamo le percentuali, aumentano in maniera consistente le nostre perdite. Anche in questo caso qualche esempio chiarirà le idee. Ci sono degli investitori che hanno comprato Tiscali a 100€ e poi le hanno viste scendere a 50€ con una perdita del 50%. Purtroppo se da 50€ Tiscali, fa un 50% di rialzo, arrivano solamente a 75€, ben lontane dai 100€ di partenza. Per vedere l’investimento tornare in pari il titolo deve raddoppiare ovvero fare un 100% di rialzo. Applicando le formule della matematica nella loro funzione relativa si ha –50% + 50% = -25%; -50% + 100% = 0.
Evidentemente è meno faticoso e più veloce fare un 50% di ribasso che un 100% di rialzo. Infatti, più sono alte le percentuali di ribasso, più aumentano le differenze richieste per compensarlo. Tiscali è scesa, dal massimo a 120€, fino a sotto i 5€ con un ribasso superiore al 90% in meno di un anno, per ritornare a quota 100€ serve un rialzo del 2000%, e quindi –90% + 2000% = 0. Quasi tutti gli investitori che hanno comprato Tiscali verso quota 100€ hanno imparato a loro spese l'importanza di adottare e applicare un piano antirischio, impiegando correttamente gli stop-loss, hanno anche imparato, a caro prezzo, che in borsa non si media mai un titolo al ribasso.
La cosa più paradossale di queste situazioni è però un'altra e, per capirla pienamente, serve un piccolo esame di coscienza da fare serenamente. Pensate per un momento a quella che è stata la vostra migliore operazione borsistica in termini percentuali. A qualcuno sarà anche capitato di fare performance a tre cifre, ma sono situazioni sicuramente non all'ordine del giorno. Poi riflettete bene su quelle che sono le vostre performance medie, quello che normalmente guadagnate operando sul mercato e, in questo caso, se non avete la faccia tosta di mentire a voi stessi, scoprirete che non si parla di performance a tre cifre, ben che vada di due.
Se però abbiamo le Tiscali (o chi per esse) in portafoglio a prezzi ormai assurdi, tutto quello che speriamo è di poter un giorno rivedere i nostri soldi; se anche solo si avvicineranno al prezzo di carico, avremmo fatto la nostra più grossa performance di tutti i tempi, senza guadagnare il becco di un quattrino.
C'è un qualcosa di perverso nelle nostre aspettative: quando impostiamo una nuova operazione ci accontentiamo di guadagnare pochi punti percentuali e ne siamo pienamente soddisfatti; sulle Tiscali speriamo che il titolo esploda al rialzo solo per poterne uscire in pari.
Non esiste un limite al rialzo di un titolo, dal collocamento a 4,6€ Tiscali ha guadagnato più del 2.600% ma anche quest’enorme rialzo si rispecchia interamente in quel 100% che è la massima perdita che può fare un titolo. Se solo riferiamo i conteggi sulle percentuali di incremento ai primi prezzi fatti segnare da Tiscali intorno ai 7€ il guadagno percentuale riferito ai massimi è sceso enormemente, dal 2.600% siamo arrivati a “solo” il 1.700%.
La matematica non è un'opinione ed è per questo che non dobbiamo farci ingannare dai preconcetti; in borsa non sempre due più due fa quattro. La nota legge della chimica di Lavoisier dice che nelle reazioni chimiche nulla si crea, nulla si distrugge ma tutto si trasforma. Purtroppo però nella trasformazione molte cose, pur non perdendosi, possono cambiare luogo di destinazione, ed è questo un evento particolarmente sgradito all'investitore se nelle combinazioni mette il suo denaro.
L’insegnamento che possiamo trarre è di renderci conto di quanto sia facile avere il pilota automatico inserito senza avere la minima cognizione sul suo funzionamento. Ben diverso è sapere in anticipo quelli saranno le nostre risposte ed i comportamenti davanti all’imprevisto, quando il pilota automatico non risponde più ai comandi.
La Borsa è un luogo ideale per i trapper, ossia per chi mette le trappole, riuscendo a sopravvivere a spese degli altri come ben sanno gli scalper professionisti. Quanto detto fa comprendere come sia particolarmente difficile recuperare le perdite, sapere che esistono i trapper e le trappole non ci salva dal rischio, ma aiuta a non esserne vittime inconsapevoli.